Angiogenesis
Background
Growth of malignant tumors beyond the diameter of 1-2 mm critically depends on their neo-vascularization, which provides vital nutrients and growth factors, and also clears toxic wasteproducts of cellular metabolism. Indeed, the role of angiogenesis – the formation of new blood vessels by budding from existing ones – as a target for cancer therapy, is currently a focus of intensive research.
In order to establish successful anti-angiogenic treatment rationale, the dynamics of angiogenesis must be better understood. These dynamics are complex, involving many interacting oscillatory processes, which operate on several scales of time and space. Having reached a certain size and, therefore, a certain critical volume/surface ratio, a shortage of oxygen (hypoxia) and nutrients is created within the tumor. Under hypoxia the tumor produces proteins, notably Vascular Endothelial Growth Factor (VEGF). Increasing VEGF levels lead to increased proliferation and mobility of endothelial cells, and, as a result, to increased formation of immature vessels by these cells. Consequently, the blood supply of the tumor is augmented, encouraging tumor proliferation.
Methods and Results
Arakelyan and colleagues studied the impact of angiogenesis on cancer progression and developed a detailed model of vascular tumor growth, which takes account of the molecular, cellular and organ level interactions in cancer cell replication, angiogenesis and vessel maturation. By mathematical and computer implementation, the model could be analyzed and numerical simulated. In this way the effects of drugs on the growth and decay of both the tumor and the immature and mature blood vessels could be evaluated, as well as on the induction of an array of relevant growth factors such as Angiopoietin-1, -2, vascular endothelial growth factor (VEGF) and platelet-derived growth factor (PDGF). The full algorithm is depicted in (Arakelyan, Vainstein, & Agur, 2002b) and in a simplified form in (Agur, Arakelyan, Daugulis, & Ginosar, 2004). How model’s equations were derived and how model parameters were calculated is accounted for in (Arakelyan, Merbl, & Agur, 2005).
Mathematical analysis and numerical simulations of the Arakelyan et al’s model shed important light on vascular tumor dynamics. Thus, it was suggested that there are circumstances in which small tumors oscillate in size instead of growing steadily. If such circumstances can be medically replicated then this may be a powerful way of controlling cancer growth (Agur, Arakelyan, Daugulis, & Ginosar, 2004; Forys, Kheifetz, & Kogan, 2005). Notably, it was suggested that monotherapy by anti-angiogenic drugs alone can slow tumor growth, but cannot altogether eliminating it, and that anti-angiogenesis drugs combined with drugs that target mature vessels may be superior to anti-angiogenic monotherapy. (Arakelyan, et al., 2002b; Arakelyan, Vainstein, & Agur, 2002a) These conclusions were later corroborated experimentally.
In order to check whether or not the model is a high-fidelity portrayal of vascular tumor growth, its predictions were experimentally validated. (Arakelyan, et al., 2005) Thus, tumor growth, neovascular maturation and functionality were studied noninvasively by magnetic resonance imaging (MRI) in human epithelial ovarian carcinoma spheroids, xenografted in mice. Individual tumor growth curves were input into the model for evaluating the tumor-specific parameters, and predictions of vascular dynamics were compared with the MRI readings. The revealed accuracy of model predictions is demonstrated in the example in Fig. 1. One can note in Fig. 1A that the model predicts complete maturation of all neovasculatures in a particular tumor, within about one month. Indeed, the experimental results support model predictions quite remarkably and further explain the model-predicted and clinically-observed short-term effects of anti-VEGF therapy (Fig. 1B).
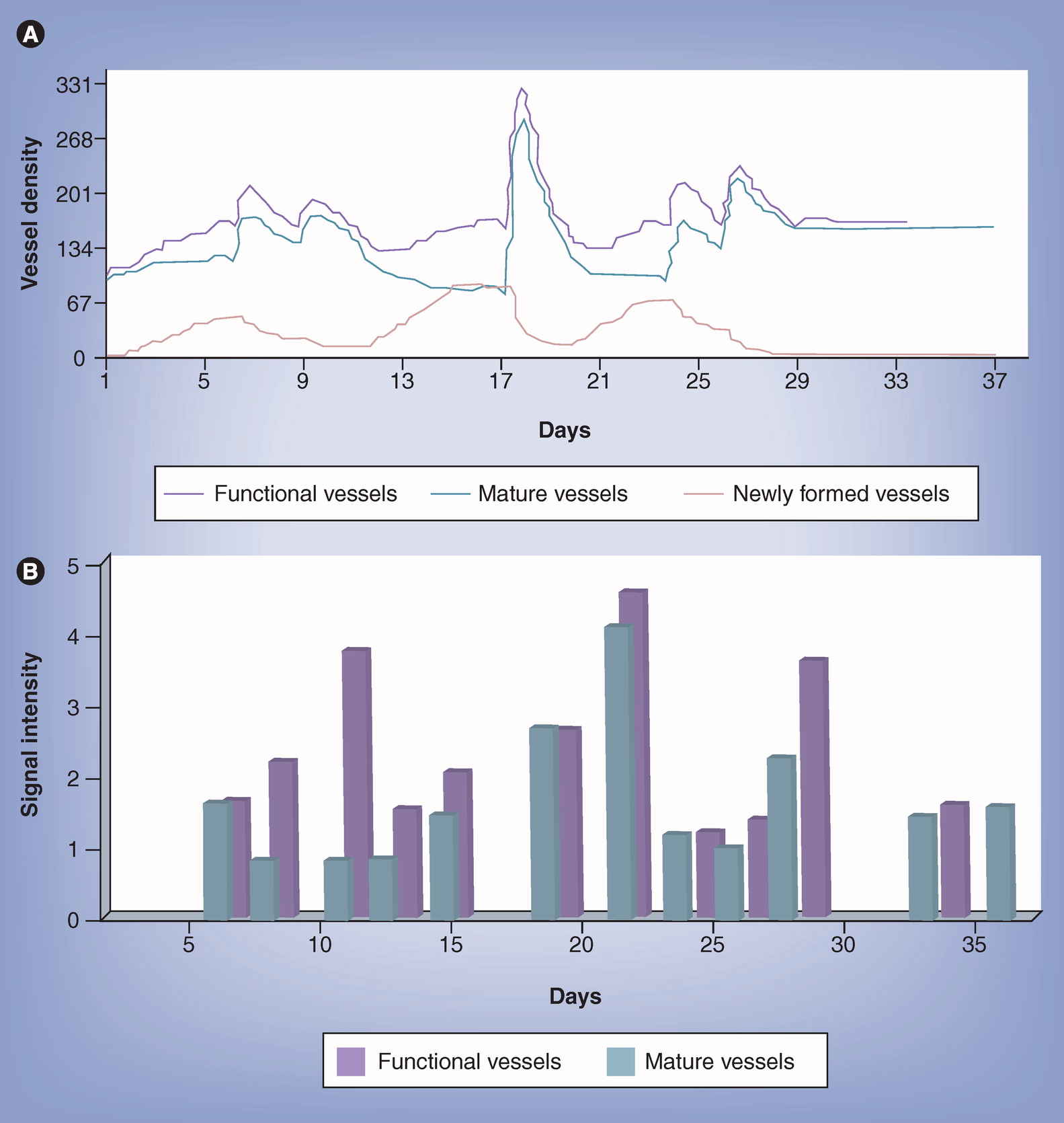
Figure 1
Prediction accuracy of the vascular tumor growth model.
In vivo validation in xenografted human Ovary Carcinoma spheroids.
A. Model predictions of neovascular and mature vessel dynamics in a single tumor, denoted “GA”
B. Experimental results of neovascular maturation and functionality in tumor “GA,” measured noninvasively by MRI; SI – signal intensity.
Conclusions
Oncologists already begin to employ methods involving mathematical models for aiding their prognostic decision-making, and drug developers already use such models for focusing clinical studies on the most promising candidates, patient-populations and treatment schedules. The transition of all the healthcare industry to model-based decision making is imminent, but not easy. New approaches will have to be adopted, integrating deep medical understanding within tools for processing complex biological dynamics. These may be an exciting period for the biomathematical science.
For further reading
- Forys, U., Kheifetz, Y., & Kogan, Y. Critical-point analysis for three-variable cancer angiogenesis models. Math Biosci Eng 2005 2(3), 511-525.
- Arakelyan, L., Merbl, Y., & Agur, Z. Vessel maturation effects on tumour growth: validation of a computer model in implanted human ovarian carcinoma spheroids. Eur J Cancer 2005 41(1), 159-167.
- Agur, Z.,Arakelyan, L., Daugulis, P., & Ginosar, Y. Hopf point analysis for angiogenesis models. DCDS-B 2004 4(1), 29-38.
- Arakelyan L. et al., Multi-Scale Analysis of Angiogenic Dynamics and Therapy, Ch. 7, in: “Cancer Modelling and Simulation”, Luigi Preziosi ed., CRC Press, LLC, (UK), 2003
- Arakelyan, L., Vainstein, V., & Agur, Z. A computer algorithm describing angiogenesis and vessel maturation and its use for studying the effects of anti-angiogenic and anti-maturation therapy on vascular tumor growth. Angiogenesis 2002 5(3), 203-214.
- Arakelyan L, Vainstain V, and Agur Z. Optimizing anti-angiogenic therapy using mathematical tools. Proceedings of American Society of Clinical Oncology (ASCO) 2002 21, p. 440a.

